Boltzmann Economy

Well, that last one was diabolical. I think I tried to do too much and I will probably never finish it, oh well. It was Mammoth! (by special request of Dr Weegink).

So I’m going to go for a nice easy one this time, revolutionizing economics. This is nothing new, but should be fun.

The Details Probably Don’t Matter

I find statistical mechanics sort of mystifying and beautiful. I find economics sort of stupefying and ugly. So let’s conflate the two to make something mystifying and ugly. The basic idea in statistical mechanics is that we worry about what macroscopic quantity is conserved and maximize entropy. Simple as that, despite what your physics lecturer said about heat baths and what not. So let’s imagine a theoretical economy where the total amount of money, $M$, is constant and individual wealth is bounded between zero and infinity. We now want to see what distribution of wealth we would get if the only thing we did was maximize the entropy. This is a pretty bullshit and simple model, but we are playing economists. So our optimization problem is,

$$J = -\int_{0}^{\infty} p(x)log(p(x))dx + \lambda_{1}(\int_{0}^{\infty} p(x)dx -1) + \lambda_{2}(\int_{0}^{\infty}xp(x)dx - M/N)$$

where $N$ is the total number of people, $p(x)$ is the probability of having $x$ wealth, $\lambda_{1}$ is a Lagrange multiplier to make the probability integrate to 1 and $\lambda_{2}$ is a Lagrange multiplier to keep the mean wealth at $M/N$. Turning the crank, you can find that the distribution that maximizes the above constrained optimization problem is our old friend the exponential distribution, i.e.

$$p(x) = N/Me^{-xN/M}$$

defined on $x \ge 0$. Well, that was a bit too easy. Does it work? Well, I actually struggled to get good data to do anything super quantitative, but subjectively you can eyeball the following figure and see that it isn’t too bad a model, apart from some poor buggers at negative wealth and a bigger than expected spike at zero (or is it a flat bit from 100-400k?).

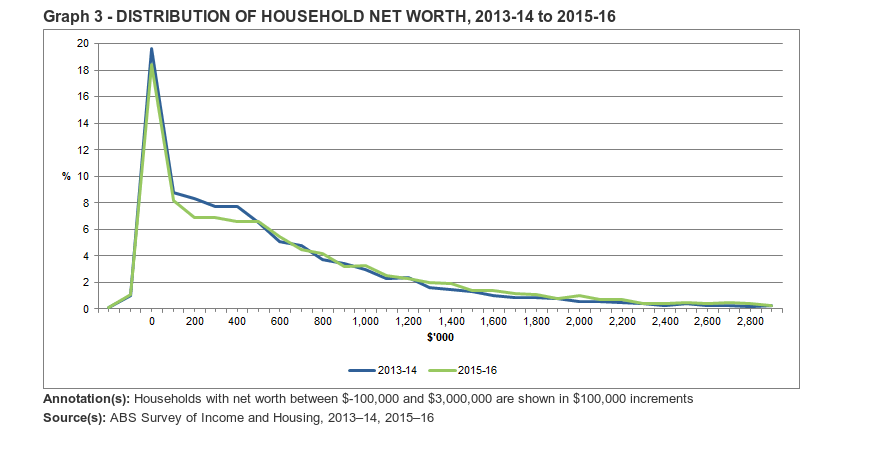
So wow, for all our economic theories, political ideology and government institutions, you can to first order approximate the real economy with a capped amount of money and model of “do whatever the fuck you want, be as random as you can be”. I can’t tell if that is liberating or depressing…

People Who Can Eat People Are The Luckiest People

So, to be fair it doesn’t explain everything. We all know that the real distribution of wealth has correlations in time and space and race and gender. It would be interesting to extend the model to find the minimal complexity model that could reproduce these features. But we don’t make models for their own sake, the real question is what can we change in this model to make it like the world we want to live in. Most would agree that an exponential distribution of wealth is unfair, we probably want something flatter but not too flat. We have a notion that we “deserve” to be rewarded, even if it is confusing luck with skill. At some point we need to face facts and realize that money is a related to energy use and we can’t keep growing the use of that forever without our grandchildren paying the bill. Well, one idea is to change some conserved quantities and see what it does. You can go have a look on Wikipedia for Maximum Entropy Distributions and choose one that suits your fancy. Alternatively a simple idea, and I guess it is related to the idea of a universal basic income (except for wealth and not income), is to cap the lower and upper bounds and see what that does to the distribution. Luckily this clever person has done the maths for us and we get a truncated exponential distribution of the form

$$p(x) = \frac{\alpha e^{\alpha x}} { (e^{\alpha b}-e^{\alpha a})}, x\in [a,b]$$

where you get $\alpha$ from solving

$$\mu = \frac{ \int_a^b \alpha x e^{\alpha x} dx}{(e^{\alpha b} - e^{\alpha a})} = \frac{b e^{\alpha b} - a e^{\alpha a}}{(e^{\alpha b}-e^{\alpha a})} -\frac{1}{\alpha}$$

(as shown in this mathoverflow answer). Nice. Does this look more “fair”? Luckily Keith Conrad in the shared link gives some nice plots of this distribution for various values on $\alpha$, as reproduced below (on the interval of $0$ to $1$).

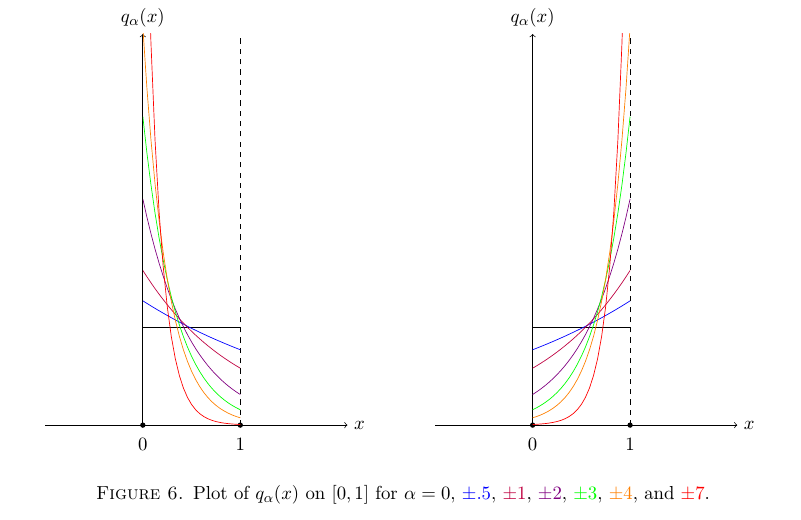
So you can have it bunch up near the boundaries depending on how close the mean quantity is to the extremes. So there you go, you can make the distribution as fair as you like, you just need to control the upper bound. Apart from the cost of enforcing such a measure, why would any reasonable person object to capping the maximum wealth of an individual, especially at a high number that isn’t infinity?

Oh well, that post was easier than the last post! I think I need to stick to spontaneous rants.