Dynamical Systems Doing Weird Shit

So this another set of notes for an IEEE journal club presentation. This time I have picked Dynamical Systems That Sort Lists, Diagonalize Matrices, and Solve Linear Programming Problems. I think this paper is super kawaii! I’m not sure if it is a practical result as it stands but it is a really interesting idea. The main idea is to approximately solve combinatorial optimization problems by solving a flow on a restricted continuous space that will have the “answer” as the final state at $t=\infty$. I came across this paper while looking into graph isomorphism in the dim mists of time, so I will use that as a lead in example.

Matching Graphs

Say you have two graphs $G$ and $H$ and they have no nodal attributes apart from an arbitrary index. However, they do have the same number of edges and the same number of nodes. Hell they even have the same degree at every node. How can you tell if these two graphs actually are isomorphic? That is, the node indices have just been shuffled around but they are actually the same graph topologically? Well if you have the corresponding adjacency matrices $A$ (of graph $G$)and $B$ (of graph $H$) then if there exists a permutation matrix $P$ such that

$$P'AP = B$$

Then they are isomorphic. This seems like a disgusting optimisation problem at face value, to have to search through all possible permutations. It is actually in the weird limbo land of being in NP but it is not known if it is in P or NP-Complete (a bit like factoring). So the idea is this, maybe if we go up a level from Permutation Matrices to Orthogonal Matrices we might be able to use our old friend calculus to help us out, since Permutation Matrices are a subset of Orthogonal Matrices. So let’s solve the following minimization problem on Orthogonal Matrices

$$J = \lVert \phi'A\phi - B \rVert_{F}^{2}$$

where $\phi$ is an Orthogonal Matrix. The optimal value should be $0$ and $\phi$ should be a Permutation Matrix if we hit the bottom, unless we hit a funny bottom (like if we have isospectral graphs that aren’t isomorphic). Now using the relationship between trace and the Frobenius norm

$$\lVert M \rVert_{F}^{2} = trace(MM')$$

and a bit of mucking around we can transform the above minimization problem into the maximization of

$$J = trace(A \phi' B \phi) + \lambda (\phi' \phi - I)$$

I have sneakily stuck in a matrix of Lagrange multipliers $\lambda$ that ensure that $\phi$ is an orthogonal matrix. After spending a reasonable amount of time staring blankly at the matrix cookbook, taking some scalar by matrix derivatives and questioning your life choices you can show that

$$\frac{\partial J}{\partial \phi} = \phi(\phi' B \phi A - A \phi' B \phi)$$

(note this has so many echos of deriving the Riccati equations of LQG control it isn’t funny). Now say we start with an initial guess at $\phi$ and we want to turn it into the right answer as we evolve the system in time. We can do this by using gradient descent, i.e.

$$\frac{\partial \phi}{\partial t} = -\phi(\phi' B \phi A - B \phi' A \phi)$$

So we just made an analog computer for solving graph isomorphism problems (apart from any grotesque errors I have made above, but you get the picture). In fact here is the real picture (which took frigging ages and still looks terrible!).

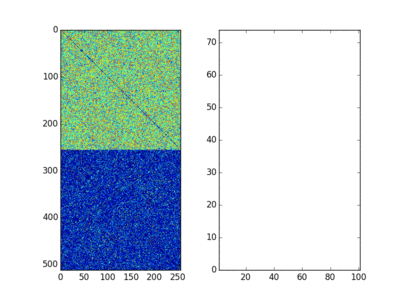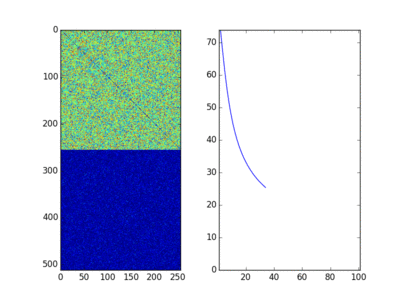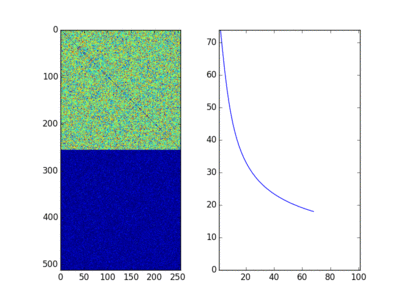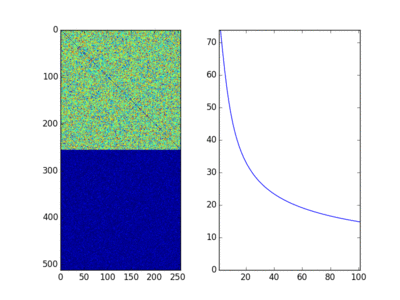
It shows the permuted adjacency matrix, the error matrix and the Frobenius Norm of the error matrix for a random $A$ and a permuted $B$. Brockett has an alternative derivation in the Appendix in the paper, but I am too dumb to ever come up with it the way he did. I need to be super explicit so the above derivation based on Lagrange Multipliers works for me. So the basic idea of the paper is that a similar “trick” will work for a whole bunch of problems like sorting and diagonalizing matrices, just with a different interpretation of $A$ and $B$. Very fun, but is it useful? Well we don’t actually have an analog computer, so we end up solving differential equations on a digital computer with the associated issues (e.g. losing Orthogonality due to numerical issues). Also this is only a local optimisation method, so it will get stuck in any old local minima or give up on flat spots. Depending on the numerical method it may converge slowly or have numerical issues. But I still think it is really cool.

Anything Else?

One thing that I though was that a little sprinkle of the old $l1$ magic wouldn’t go astray here (to push it towards a sparse $\phi$). A really interesting point that came up for me in reading the paper is his opening point about Neural Networks being analog computers. It is funny (with the context of history and having just spent a while fighting stability issues with the above system) that the dumbest possible approximation to gradient descent (that doesn’t even use all the information available) is the state of the art for training Neural Nets (i.e. SGD). It also makes me think that maybe there aren’t enough explicit constraints applied to the loss functions used for Machine Learning. For example, maybe there is an analogous constraint you could derive to enforce translation invariance for an image classifier based on Lagrange Multipliers, rather than relying on implicit invariances due to the network architecture and using data augmentation to paper up the cracks. But maybe if you alter the loss this way the manifold that the weights evolve on might be too fragile to allow SGD. Anyway, rambling now…